3D Object - Curve & Surface

2d 선, 3d 면으로 얘기 할 수 있다.

곡선과 곡면

Curve의 3가지 형태

양함수식

               y = f(x)

                  = mx + b

• 하나의 값만이 가지고 있다.
  • 하지만, 여러가지의 값을 표현할 수 는 없다.
• 특성 유지가 안된다.
• 무한의 기울기는 표현하기 어렵다

음함수식

Ax + By + C = 0

• 반원은 표현할 수 없다.
• 두개의 커브를  연결하기가 어렵다.

이 두가지 방식의 문제점을 해결하기 위해 매계변수식을 사용한다.

매계변수식

x = x(t), y = y(t), z = z(t)

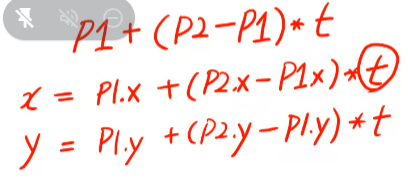
• 양함수, 음함수 식의 문제를 해결했다.
• 기울기를 tan 벡타를 사용한다.
• 무한한 기울기를 표현할 수 없다.
• 근사치를 구한다.

tangent vector

 

Curves의 3가지 타입

• Hermite
  
  • 두 끝점과 끝점은 tangent vector로 되어있다.
  • 점의 기울기가 tangent vector이다.

  • 

• Bezier
  • 두 개의 끝점과 두 개의 다른 점에 의해 정의됨

  • 

• Spline
  • 4개의 점으로 정의된다.  
    • B-스플라인, 불균일한 B-스플라인, ß-스플라인

Bezier 곡선 특징

• 첫번째 점과 마지막 점은 곡선에 포함된다.
• 곡선이 convexhull안에 존재한다.
• Local control을 못한다.
  • 전역적으로 모델이 바뀐다. 그 뜻은 모든 곡선에 영향을 준다. 부분적으로 영향을 주지는 못한다.
  • 그래서 3D 모델링에는 적합하지 않는다.

B-spline 곡선의 특징

• 4가지 점을 조절 할 수 있다.
• convexhull의 성격을 가지고 있다.
• 부분적으로 곡선에 영향을 줄 수 있다.
  • 모델링에 적합하다.

기하학적 연속성

G0 기하학적 연속성

두 곡선 세그먼트가 결합

G1 기하학적 연속성

두 세그먼트의 tangent vector의 방향이 join 점에서 동일하다.

- >반드시 크기는 아니다.

모수 연속성

C1모수 연속성

두 곡선 세그먼트의 tangent vector가 조인 점에서 동일하다.

-> 방향과 크기

Cn 모수 연속성

n번째 도함수(n차미분)를 통한 dn/dtn[Q(t)]의 방향과 크기는 결합점에서 같다.

Subdivision(소분)

정확한 값을 구하는 것보다, 근사치 값을 구하는 것이 훨신 간단하다.

Biparametric patch(양극 패치)

Joining Two patch

• C0 연속성을 사용하려면 경계 곡선을 정렬해야 합니다.
• C1 연속성은 경계 곡선과 도함수를 정렬하는 것을 필요로 한다.