그래프(Graph)

Graph

G = (V , E)

• G : 그래프
• V : 정점(vertex)의 집합
• E : 정점들을 잇는 간선(Edge)의 집합

Graph의 종류

• 간선의 뱡향성 유무
  • 비방향(undirected) 그래프 == 양뱡향
  • 방향(directed) 그래프
• 간선의 가중치(숫자) 유무
  • 가중치(weighted) 그래프
  • 비가중치 그래프

Graph 용어

경로(path)

- 어떤 정점에서 다음 정점을 잇는 이음선(간선)이 존재하는 일련의 정점

- 단순 경로(simple path) : 같은 정점을 두 번 거치지 않는 경로

- 경로의 길이 : 경로상의 간선의 수

싸이클(cycle)

- 어떤 정점에서 그 정점 자신으로 가는 경로

- 싸이클 존재 유무 : cyclic 그래프 vs acyclic(싸이클이 하나도 없어야 한다.) 그래프

- tree : 싸이클이 없는 연결 그래프(정점이 다 연결되어 있지 않는 것)

차수(degree) : 해당 정점의 간선의 수

인접(adjacent) : 두 정점 사이에 간선이 존재한 것

연결(connected) : 두 정점 사이에 경로가 존재한 것

예)

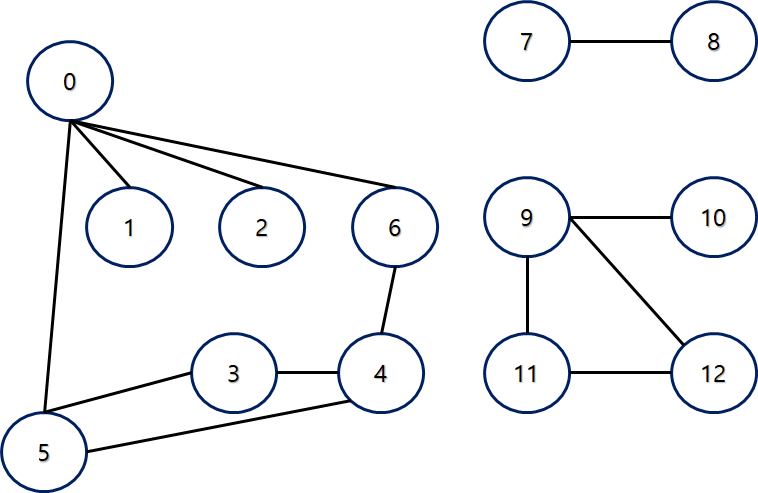
V = {0 1 2 *** 12}

|V| = 13

|V| (Cardinality) -> 집합의 원소가 몇 개인가

 

E = 그림 확인

|E| = 26(양방향을 고려해야 한다.)

 

차수가 가장 많은 정점 : 0 (4개)

비방향 그래프

가중치가 없다.

연결 컴포넌트 수 = 3

(연결되어있는 정점들의 부분 집합)

순환 그래프

Graph 표현

행렬

정점의 개수가 n인 그래프를 n*n 행렬로 표현

array[i][j]

{

      if 1 // 정점 i와 정점 j가 인접한 경우

      if 0 // 정점 i와 정점 j가 인접하지 않는 경우

}

항상 n^2에 비례하는 공간이 필요하다.

간선의 밀도가 높은 고밀도 그래프(dense graph)에 적절하다.

인접 리스트(연결 리스트 사용)

정점의 개수가 n인 그래프를 n개의 연결 리스트 배열로 표현

정점에 인접한 정점들을 연결리스트에 저장

정점의 개수에 비해 간선의 수가 적은 저밀도 그래프(sparse graph)에 적절하다

-> 실생활에서는 대체로 저밀도 그래프이다. 지하철 노선

비방향 그래프

그래프의 탐색(Graph search) = 그래프 순회(Graph traversal)

간선을 따라 한 번씩 방문하는 것

DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)

탐색에 필요한 배열

• vis[0 ~ n - 1] : 정점별 방문 여부, 방문했으면 Yes(1), 아니면 No(0)
• edgeTo[0 ~ n - 1] : 탐색(순회) 간선(edgeTo[i] -> i)
• 그래픽 탐색의 결과는 edgeTo[] 간선으로 이루어진 tree이다.

DFS(Depth-First Search : 깊이우선탐색)

• 시작 정점을 방문한 후, 인접한 정점들 중 방문하지 않은 정점을 다시 시작 정점으로 하여 재귀적으로 깊이우선탐색
• 방문하지 않은 정점은 STACK(LIFO)에 삽입한다
• 미로 탐색과 유사하다.
• 활용
  • 포토샵의 Flood fill

BFS(Breadth-First Search : 너비우선탐색)

• 시작 정점으로부터 가까운 정점들을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법(재귀가 아니다)
• 방문한 정점과 인접한 정점들 중 방문하지 않은 정점을 QUEUE(FIFO)에 삽입
• 활용
  • BFS는 시작 정점으로부터 다른 정점까지의 간성의 수를 최소로 하는 경로를 구한다.
  • 라우팅
  • 케빈 베이컨 수(Kevin Bacon number)

방향 그래프(Digraph : directed graph)

방향 그래프에서의 DFS

활용 사례

• 프로그램 제어 흐름(control-flow) 분석
  • 제어문(조건문, 반복문) : 문장(statment) 실행 순서문
• 가비지 콜렉터(garbage collector)
  • 가비지 : 아무도 쓰지 않는 메모리
  • 도달 가능한 객체를 마킹한 후, 마킹되지 않은 모든 객체는 청소
• DAG(Directed acyclic graph)
  • 위상정렬(topological sorting)
    • 주어진 방향 그래프(작업의 선후 관계)로 부터 작업 스케줄링 하기
    • 예)
      • 0 : 1 2 5
        1 : 4
        2 : 
        3 : 2 4 5 6 
        4 : 
        5 : 2
        6 : 0 4
        
        DFS를 하면?
        4 1 2 5 0 6 3
        
        트리 순회 한다 (후위)
        3 6 0 5 2 1 4
        
        -> DAG에 사용된다.