-
최적화 문제란?
최적값을 구하거나 최적값에 해당하는 후보해답(=최적해: 정해진 답을 구하는 방법)을 구하는 문제
예)
- 최단경로 문제 : 한 정점에서 다른 정점으로 가는 경로들 중 가장 거리가 짧은 경로
- 배낭 채우기 문제 : 배낭의 용량을 초과하지 않으면서 가치를 최대로 배낭에 물건을 채우는 방법 (0-1 배낭문제 vs 연속 배낭문제
해법
- 무작정 알고리즘(brute-force search)
- 모든 가능한 경우를 탐색하여 최적화 구하기
- 흔히 지수시간 알고리즘
-> 가능하면 사용하지 않는 것
- 주로 동적프로그래밍 혹은 탐욕적 방법을 사용
- 두 방법 중 하나로 해결되는 경우, 알고리즘은 흔히 다차시간(polynomial time) 소요
- 많은 최적화 문제는, 다차시간 알고리즘을 구해지 못했고 다차시간 알고리즘이 존재하지않음도 증명하지 못함 (NP-complete) -> 많은 문제가 그러하다.
다차시간 알고리즘이 없는 문제는 최대한 효율적으로 최적해를 구하거나 근사해를 구함
-> 항상 최적값을 먼저 구하고 최적해를 구성(traceback)하는 전략 사용해야 함
동적프로그래밍(dynamic programming)
- 동적프로그래밍 알고리즘의 개발 절차
- step 1 : 큰 문제에 대한 해와 작은 문제에 대한 해 사이의 재귀관계식을 정립
- step 2 : 작은 문제를 먼저 해결한 결과를 큰 문제의 해결에 사용
동적프로그래밍 vs 분할정복
분할 정복 알고리즘
- 하향식(top-down) 접근 방법
- 부분 문제들이 서로 독립적인 문제로 분할될 때 유용
동적프로그래밍
- 작은 문제를 먼저 해결한 후 그 결과를 저장하여 더 큰 문제의 해결에 반복적으로 적용
- 상향식(bottom-up) 접근 방법
- 부분 문제들이 서로 독립적이지 않고, 부분 문제들이 다시 자신의 부분 문제를 공유할
때 유용
예)
피보나치 수열 : 분할정복 vs 동적프로그래밍
분할정복
fib1(n)
if (n==0 || n==1) return n;
return fib1(n-1) + fib1(n-2);-> 지수 시간이 걸린다
동적프로그래밍 알고리즘
fib2(n)
f[0...n] 공간 확보;
f[0] = 0; f[1] = 1;
for (i=2; i<=n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];-> O(n) 시간 소요!!!!!
-> 중복되는 재귀호출이 발생하는 경우에는 재귀식을 하향식으로 사용하는 분할정복법 대신동적프로그래밍을 사용하여야 함
동적프로그래밍과 최적화 문제
최적의 원칙(principle of optimality)
동적프로그래밍으로 최적화 문제를 풀기 위해서는 최적의 원칙을 만족해야 한다.
큰 문제에 대한 최적해가 부분문제에 대한 최적해를 항상 포함하는 것을 일컫는다.
최단경로문제 : 최단경로상의 모든 부분경로들 역시 해당 정점들에 대하여 최적이다.
최장경로문제 : 최장경로상의 부분경로가 반드시 두 점상의 최장경로는 아니다.최장 공통 부분순서 문제
최장 공통 부분순서(LCS: Longest Common Subsequence)
두 문자열에 공통적으로 나타나는 부분 순서들 중 가장 긴 것
Sequence
- : 순서를 갖는 것
- : 수열, 문자열
- 예) cats
Subsequence
- : 순서를 갖는 부분
- : 순서가 연속적 X
- 예) ca, ats, ct, cs
common(공동의) Subsequence
- : 공동의 순서를 가진 부분
- : 2개 이상의 sequence가 필요하다.
- 예) "at, a, t, 공집합"
-> L(Longest: 가장 긴)C(Common)S(SubSequence)
가장 긴 길이의 공통된 부분 -> 2개 이상의 시퀀스에서 공통적으로 가진 것들
--> 최적값에 집중해야 한다.
예) 위의 예를 종합: LCS: 2 ("at")
LCS(의 길이)에 존재하는 최적 부분구조
X[m] = {x1,x2, ~ xm}, Y[n] = {y1,y2 ~ yn} LCS의 길이 Z[k][r] int i = 0 // X의 부분 검색 범위 int o = 0// Y의 부분 검색 범위 if (X[i] == Y[o]) { k[i][o] = K[ i - 1 ][ o - 1 ] + 1 } else if (X[i] != Y[o]) { Max(LCS(X[ i - 1 ], Y[o]), LCS(X[i], Y[ o - 1 ])) }동적 프로그래밍 -> 동적 다이나믹으로 풀게 된다.
LCS를 구하는 분할 정복 알고리즘: 재귀 알고리즘으로 하면 오래 걸린다.
테이블 Z를 이용해서 역추적(traceback or backtrack)하여 구할 수 있다.
최장 부분순서의 길이는 유일하지만, 그 길이를 갖는 최장 부분순서는 여러 개존재할 수 있다.
최장 부분순서 문제의 활용
- 유닉스 diff utility : 라인 기반의 파일 비교(file comparison) 유틸리티
- Screen redisplay in “emacs” : 터미널에 가능한 적은 숫자의 문자를 업데이트
- Revision control system(e.g. Git)
연산의 종류: deletion, insertion
- LCS는 deletion과 insertion만을 허용하는 편집 거리 문제의 특별한 경우이다.
- d(X(m) , Y(n)) = m + n - 2 * LCS(X(m) , Y(n)0-1 배낭문제
배낭문제 (knapsack problem)
- 배낭에 담을 수 있는 n개 아이템의 아이템별 무게와 가치가 주어 짐
- w[i] : i번째 아이템의 무게
- p[i] : i번째 아이템의 가치
- C : 배낭에 넣을 수 있는 최대 무게(용량)
-> 목표: 용량을 초과하지 않으면서, 배낭에 담는 아이템의 가치의 합이 최대가 되도록 담는 것이다.
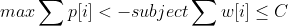
0-1 : 아이템의 부분을 배낭에 넣는 것이 불가능하다
- 넣고 빼고만 가능
- 아이템의 부분을 넣는 것이 불가능
- 풀기 어렵다-> 다차시간 알고리즘이 존재X
연속 : 아이템의 부분을 배낭에 넣는 것이 가능
- 부분적으로 넣을 수 있다.
0-1 배낭문제를 푸는 동적프로그래밍 알고리즘
Pack[i][c] : 현재 남은 공간이 c일 때, 아이템 번호 (0, ..., i)에서 아이템을 선택하여 가질수 있는 최대 가치
- i번째 아이템을 선택하는 경우 : Pack[i - 1][c-w[i]] + p[i]
- 0 ~ i - 1 : 아이템 선택권
- c - w[i] :남아있는 용량
- i번쨰 아이템을 선택하지 않는 경우 : Pack[i-1][c]
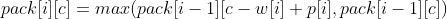
재현식: For i = 1, ...., n - 1, c = 0, ... , C
최적해(=최적 가치) : pack[n - 1][C]
시간복잡도: O(n * C)
-> n과 비교하여 C가 극도로 큰 경우에는 모든 부분집합을 고려하는 알고리즘보다 나쁨
-> 배낭의 크기에 시간복잡도에 영향을 준다.
-> 0-1 배낭문제는 대표적 NP-complete(완비) 문제이다