서포트 벡터 머신

선형 SVM

Support Vector Machine

• 분류 문제에서 일반화(generalization)능력이 입증되어 머신러닝 알고리즘에서 인기가 높다
• 선형 또는 비선형 분류뿐만 아니라 회귀, 이상치 탐색에도 사용된다.
• 복잡한 분류 문제와 잘 맞고, 중간 크기의 데이터 셋

소프트 마진 SVM

• Support vectors가 위치한 경계선에 여유를 두자
• 여유 변수 (Slack Variable)
• C 라는 하이퍼파라미터 제공(penalty)

Slcak 변수와 규제

• C 값을 줄이면 오류를 허용하는 정도가 커지며 , Margin 또한 커진다
• C 값을 크게하면 오류를 허용하는 정도가 작아지며 , Margin 또한 작아진다

비선형 SVM

• 선형적으로 분류할 수 없는 데이터 셋이 존재한다.
• 다항 특성과 같은 특성을 추가

다항 특성 사용한 SVM

다항 특성을 사용해서 표현한다.

커널 트릭 사용

다항식 특성들이 추가되면 모델 속도가 느려진다. 속도 저하를 해결하기 위해 커널 트릭을 이용한다.

SVM 회귀

• 분류와 반대
• 마진의 밖이 오류에 해당 , 마진 안쪽으로 최대한 많은 데이터들이 포함되도록

선형 회귀

비선형 획귀

SVM 이론

여백(margin)의 크기는 일반화하고 관련이 있다.

마진을 최대화 하는 결정 초평면을 찾는 것이 목표이다.

• 3번이 두 클래스를 잘 나누고 있다.
• wx + b =0 이 구간은 나눈는 경계선이다.

w : 초평면의 법선의 벡터
b : y절편

Margin

목표

마진을 가장 크게 하는 결정 초평면을 찾는 것이다.

w 를 찾는 것이 목표

손실 함수

최대 마진을 구하는 문제에 역수를 취해 최소화 문제

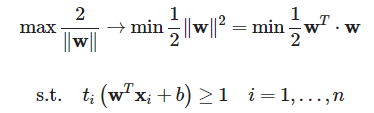
Soft margin

Soft Margin SVM

Slack 변수를 추가한 소프트 마진의 목적함수(min뒤에 나온 부분이다.)

소프트 마진의 제약식

Kernel SVM

• 선형으로 분리되지 않는 데이터를 비선형 매핑
• 저차원에서 고차원으로의 매핑을 통해 해결한다.

두개의 벡터(데이터)를 입력을 가진다.

k(a,b) 형태이다.

L 공간 상의 두 벡터 a 와 b 를 입력 변수로 갖는 커널 함수 K( a,b ) 는 K( a,b )=Φ(a) Φ(b)를 만족하는 매핑 함수 Φ(⋅) 가 존재해야 함

2차 다항식 매핑